CPN (Counterpropagation Network)

May 26 • General • 14843 Views • 7 Comments on CPN (Counterpropagation Network)

CPN (COUNTERPROPAGATION NETWORK):

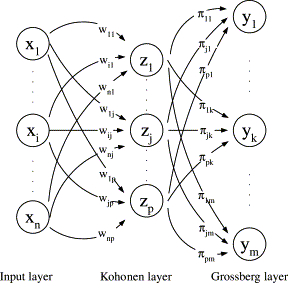
CPN (Counterpropagation network) were proposed by Hecht Nielsen in 1987.They are multilayer network based  on the combinations of the input, output, and clustering layers. The application of counterpropagation net are data compression, function approximation and pattern association. The ccounterpropagation network is basically constructed from an instar-outstar model. This model is three layer neural network that performs input-output data mapping, producing an output vector y in response to input vector x, on the basis of competitive learning. The three layer in an instar-outstar model are the input layer, the hidden(competitive) layer and the output layer.

There are two stages involved in the training process of a counterpropagation net. The input vector are clustered in the first stage. In the second stage of training, the weights from the cluster layer units to the output units are tuned to obtain the desired response. There are two types of counterpropagation net:

1. Full counterpropagation network

2. Forward-only counterpropagation network

Full counterpropagation network:

Full CPN efficiently represents a large number of vector pair x:y by adaptively  constructing a look-up-table. The full CPN works best if the inverse function exists and is continuous. The vector x and y propagate through the network in a counterflow manner to yield output vector x* and y*.

Architecture of Full CPN:

The four major components of the instar-outstar model are the input layer, the instar, the competitive layer and the outstar. For each node in the input layer there is an input value xi. All the instar are grouped into a layer called the competitive layer. Each of the instar responds maximally to a group of input vectors in a different region of space. An outstar model is found to have all the nodes in the output layer and a single node in the competitive layer. The outstar looks like the fan-out of a node.

Training Algorithm for Full CPN:

Step 0: Set the weights and the initial learning rate.

Step 1: Perform step 2 to 7 if stopping condition is false for phase I training.

Step 2: For each of the training input vector pair x:y presented, perform step 3 to .

Step 3: Make the X-input layer activations to vector X.

Make the Y-input layer activation to vector Y.

Step 4: Find the winning cluster unit.

If dot product method is used, find the cluster unit zj with target net input; for j=1 to p,

zinj=∑xi.vij + ∑yk.wkj

If Euclidean distance method is used, find the cluster unit zj whose squared distance from input vectors is the smallest:

Dj=∑(xi-vij)^2 + ∑(yk-wkj)^2

If there occurs a tie in case of selection of winner unit, the unit with the smallest index is the winner. Take the winner unit index as J.

Step 5: Update the weights over the calculated winner unit zj.

For i=1 to n,  viJ(new)=viJ(old) + α[xi-viJ(old)]

For k =1 to m,  wkJ(new)=wkJ(old) + β[yk-wkJ(old)]

Step 6: Reduce the learning rates.

 α (t+1)=0.5α(t);  β(t+1)=0.5β(t)

Step 7: Test stopping condition for phase I training.

Step 8: Perform step 9 to 15 when stopping condition is false for phase II training.

Step 9: Perform step 10 to 13 for each training input vector pair x:y.  Here α and β are small constant values.

Step 10: Make the X-input layer activations to vector x. Make the Y-input layer activations to vector y.

Step 11:  Find the winning cluster unit (Using the formula from step 4). Take the winner unit index as J.

Step 12: Update the weights entering into unit zJ.

For i=1 to n,  viJ(new)=viJ(old) + α[xi-viJ(old)]

For k =1 to m,  wkJ(new)=wkJ(old) + β[yk-wkJ(old)]

Step 13: Update the weights from unit zj to the output layers.

For i=1 to n,  tJi(new)=tJi(old) + b[xi-tJi(old)]

For k =1 to m,  uJk(new)=uJk(old) + a[yk-uJk(old)]

Step 14: Reduce the learning rates a and b.

a(t+1)=0.5a(t);  b(t+1)=0.5b(t)

Step 15: Test stopping condition for phase II training.

Forward-only Counterpropagation network:

A simplified version of full CPN is the forward-only CPN. Forward-only CPN uses only the x vector to form the cluster on the Kohonen units during phase I training. In case of forward-only CPN, first input vectors are presented to the input units. First, the weights between the input layer and cluster layer are trained. Then the weights between the cluster layer and output layer are trained. This is a specific competitive network, with target known.

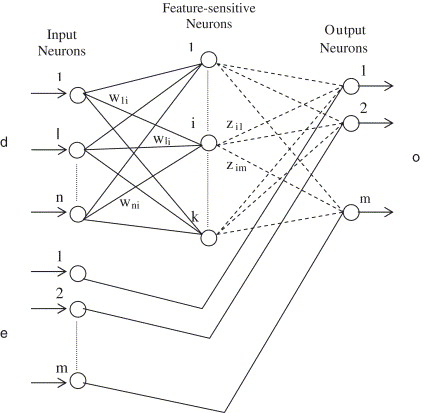
Architecture of forward-only CPN:

It consists of three layers: input layer, cluster layer and output layer. Its architecture resembles the back-propagation network, but in CPN there exists interconnections between the units in the cluster layer.

Training Algorithm for Forward-only CPN:

Step 0: Initialize the weights and learning rates.

Step 1: Perform step 2 to 7 when stopping condition for phase I training is false.

Step 2: Perform step 3 to 5 for each of training  input X.

Step 3: Set the X-input layer activation to vector X.

Step 4: Compute the winning cluster unit J. If dot product method is used, find the cluster unit zJ with the largest net input:

zinj=∑xi.vij

If Euclidean distance is used, find the cluster unit zJ square of whose distance from the input pattern is smallest:

Dj=∑(xi-vij)^2

If there exists a tie in the selection of winner unit, the unit with the smallest index is chosen as the winner.

Step 5: Perform weight updation for unit zJ. For i=1 to n,

viJ(new)=viJ(old) + α[xi-viJ(old)]

Step 6: Reduce learning rate α:

α (t+1)=0.5α(t)

Step 7: Test the stopping condition for phase I training.

Step 8: Perform step 9 to 1 when stopping condition for phase II training is false.

Step 9: Perform step 10 to 13 for each training input pair x:y.

Step 10: Set X-input layer activations to vector X. Set Y-output layer activation to vector Y.

Step 11: Find the winning cluster unit J.

Step 12: Update the weights into unit zJ. For i=1 to n,

viJ(new)=viJ(old) + α[xi-viJ(old)]

Step 13: Update the weights from unit zJ to the output units.

For k=1 to m,   wJk(new)=wJk(old) + β[yk-wJk(old)]

Step 14: Reduce learning rate β,

β(t+1)=0.5β(t)

Step 15: Test the stopping condition for phase II training.

CPN

« Biological Neuron Artificial Neuron Solar Radiation »