Depth First Search and Breadth First Search (BFS and DFS)

May 26 • General, Notes • 6509 Views • 33 Comments on Depth First Search and Breadth First Search (BFS and DFS)

Depth First Search and Breadth First Search (BFS and DFS)

Depth First Search and Breadth First Search are two simple tree traversal techniques which are commonly used in areas problem spaces (discussed earlier here) related to Artificial Intelligence or AI. Now both will be discussed in detail.

Breadth First Search (BFS)

In this method of searching in a graph, specially a  tree, search is limited to three possible operations:

1. Visit and inspect (process) a node of a graph
2. Gain access to visit the nodes which are the neighbor of the current node
3. If there are no more neighbors go to the next level

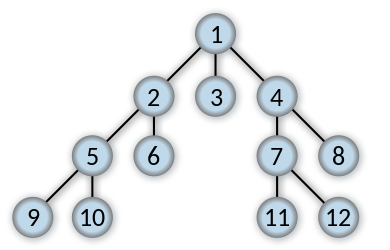
This begins at a root node, inspecting all the neighboring nodes. Then for each of those neighbor nodes in turn, it inspects their neighbor nodes which were unvisited, and so on. And when all the nodes in a particular level are visited inspection moves to the next level. The numbering order shows the order of traversal in BFS.

Depth First Search and Breadth First Search

Worst case performance          :   O(|E|) = O(b^d)
Worst case space complexity  :   O(|V|) = O(b^d)

Depth First Search (DFS)

Depth-first search or DFS is a traversing or searching  technique for tree or graph data structures. In this the processing starts at the root (selecting some node as the root in the graph case) and exploring as far as possible along each branch before backtracking is done.It can also be said to be an uninformed search that progresses by expanding the first child node of the search tree that appears, going deeper and deeper until a goal node is found, or it hits a node that has no children. Then the processing backtracks, returning to the most recent node it hasn’t completely explored. The search technique can thus be outlined as:

1. Process the current node to find its child node.
2. Go on processing a child nodes till the goal state is obtained or till there are no more child node
3. Backtrack to the last node which had 2 or more child nodes

BFS and DFS Techniques by oureducation.in

The traversal order is shown in this diagram for better understanding.

Depth First Search and Breadth First Search

Worst case performance     O(|E|) for explicit graphs traversed without repetition,
O(b^d) for implicit graphs with branching factor b searched to depth d

Worst case space complexity   O(|V|) if entire graph is traversed without repetition,
O(longest path length searched) for implicit graphs without elimination of duplicate nodes

For more articles visit www.oureducation.in and blog.oureducation.in

« Introduction TO Wireless Network Biological Neuron Artificial Neuron »