IMAGE TRANSFORM

Jun 17 • Notes • 4501 Views • 4 Comments on IMAGE TRANSFORM

IMAGE TRANSFORM

Depending on the transform chosen an operator or function selects an image as input and produces an image as output. KL analysis, fourier transforms and various spatial filters are image transformation procedure.

 

HAAR TRANSFORM

One of the simplest wave transform is Haar transform. Fourier transform cross multiplies a function against with two phase and many stretches against  sine wave same as Haar transform cross multiplies a function with various shift and stretches against the Haar wavelet.

It is a transform which is derived from the Harr matrix. It is a kind of sampling process in ehich transformation matrix rows  behaves as a sample of finer resolution.

Example of Haar transform matrix

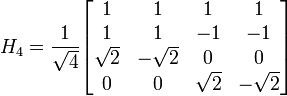
H_4 = \frac{1}{\sqrt{4}}<br /><br /><br /><br /><br /> \begin{bmatrix} 1 & 1 & 1 & 1 \\ 1 & 1 & -1 & -1 \\ \sqrt{2} & -\sqrt{2} & 0 & 0 \\ 0 & 0 & \sqrt{2} & -\sqrt{2}\end{bmatrix}<br /><br /><br /><br /><br />

SLANT TRANSFORM

Slant transform is developed by Pratt et al and introduced by Enomoto and Shibata in 1971.

[V] = [Sn][U][Sn]r

It is a 2D slant transform. Where, U is the original image of size N X N. and Sn is the unitary slant matrix.

This transform is a member of orthogonal transform. And for the first row it has a constant function and for the second row it has a linear function of the column index.

Properties of slant transform:

  • Real and orthogonal
  • Fast transform
  • Good energy compaction

KL TRANSFORM

KL transform is introduced by the Karhunen and Louve for continuous random process as a series expansion. It is an adaptive technique of signal processing and it is a tool used for data compression and pattern recognition.

Properties of KL transform are

  • KL transform decorrelates the process
  • Total mean square is minimized by the KL expansion
  • Explained variance
  • Representation entropy property is minimum

2-D Discrete Fourier Transform(DFT)

2-D DFT of an NxN image {u(m, n)} Is given as

N −1 N −1 v ( k , l ) = ∑∑ u ( m, n )WN WN n , km l 0 ≤ k, l ≤ N −1 m =0 n =0

and it is a seperable transform.

And inverse transform of 2D DFT is given as

N −1 N −1 v ( k , l ) = ∑∑ u ( m, n ) WN WN n , km l 0 ≤ k, l ≤ N −1 m=0 n =0

PROPERTIES OF 2D DFT:

  • Conjugate symmetry
  • Symmetric and unitary
  • It is a fast transform so 2-D DFT is separable.

SAMPLING THEOREM

Sampling theorem is also known as Nyquist-Shanon sampling theorem. This theorem is given by Harry Nyquist and Claude Shanon.

Sampling is a process of converting continuous time or space function into discrete time or space functionor converting a signal into a numeric sequence.

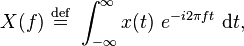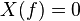X(f)\ \stackrel{\mathrm{def}}{=}\ \int_{-\infty}^{\infty} x(t) \ e^{- i 2 \pi f t} \ {\rm d}t,     and X(f) = 0 \quad   for all  |f| > B.\,

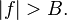
Where, X(f) is the fourier transform of function x(t) which is band limited. And at the intervals of T seconds when x(t) is sampled uniformly then result is denoted by x(nT) and the sample rate is given by

fs  = 1/T

fs > 2B and B < fs / 2 is the sufficient condition to reconstruct the x(t) where, 2B is the Nyquist rate and fs / 2 is the Nyquist frequency. The condition described by these inequalities are called as Nyquist criterion.

QUESTION AND ANSWER

  1. What is an image transform??

ANSWER

Depending on the transform chosen an operator or function selects an image as input and produces an image as output

2. What are the image transformation procedure??

ANSWER

Image transformation procedure are

KL analysis, fourier transform and various spatial filters.

3. What are the properties of slant transform??

ANSWER

Properties of slant transform are

  • Good energy compaction
  • Fast transform
  • Real and orthogonal

4. What is sampling??

ANSWER

Sampling is a process of converting continuous time and space function into discrete time and space function. Sampling theorem is also known as Nyquist-Shannon sampling theorem and it is named after Harry Nyquist and Claude Shanon.

GATE Syllabus-

1. Gate Syllabus for Electronics and Communication 2014

2. Gate Syllabus for Engineering Science 2014

IES Syllabus-

1. IES Syllabus for General ability

2. IES Syllabus for Electronics and Telecomm

About the Author:

I am Passionate Content Writer. I have worked for Many Educational Firms in the Past. I Have done Journalism in Print Media. I also have done MBA from MICA. I am fun Loving Person and Believes in Spreading the Knowledge among people. I belong to Amritsar, Punjab

Tell us Your Queries, Suggestions and Feedback

Your email address will not be published.

4 Responses to IMAGE TRANSFORM

  1. Seetha Manoharan says:
    at

    it is a good article. it clearly explains different transform concepts.

    Reply
  2. Dinesh says:
    at

    kaleidoscopic experiment explained very beautifully in theoretically.
    this article explains the difficult task very easily

    Reply
  3. Madhan says:
    at

    Image transform is one of the process of making graphical image processing and this is the emerging field. This article helps to know from basics of image transform.

    Reply
  4. Shivangi Nupur says:
    at

    students should be well aware about the various types of transforms as some of these found its daily application in maths and physics

    Reply

« »